Clasificación de eventos
Contenido
6.1. Clasificación de eventos¶
Para comparar con los algoritmos de las LHCO 2020, utilizamos como base algunos algoritmos sencillos ya implementados en librerías como scikit-learn[119] y uno programado usando TensorFlow[120]. En esta sección, se observarán algunas de las características de la clasificación realizada con estos algoritmos. Los modelos utilizados son los presentados en la Tabla 6.1, explicados en la Sección 4.2.
Nombre |
Implementación |
Algoritmo |
Tipo |
|---|---|---|---|
Random Forest Classifier (RFC) |
|
Supervisado |
|
Gradient Boosting Classifier (GBC) |
|
Supervisado |
|
Quadratic Discriminant Analysis (QDA) |
|
Supervisado |
|
MLP Classifier |
|
Supervisado |
|
Tensorflow Classifier |
|
Supervisado |
|
KMeans |
|
No supervisado |
Para el entrenamiento de los modelos y realizar las predicciones se utilizaron las variables descritas en la Tabla 4.4, a excepción de las variables de masa (\(m_{jj}\), \(m\_{j_1}\) y \(m\_{j_2}\)), con el fin de intentar una clasificación libre de modelo en lo que respecta a la masa de las partículas.
6.1.1. Conjunto R&D¶
Los datos del conjunto R&D se dividieron en conjuntos mutuamente excluyentes: 70% en un conjunto de entrenamiento y 30% en uno de prueba. A continuación, se mostrará la importancia de las variables para la clasificación según RFC y GBC y se observarán las distribuciones de los eventos clasificados para algunas variables, utilizando el conjunto de prueba.
6.1.1.1. Importancia de las características¶
De los modelos en la Tabla 6.1, RFC y GBC permiten conocer cuáles de las variables de los eventos fueron las más relevantes para discriminar entre clases. Estos algoritmos asignan puntajes a las variables de acuerdo a su importancia para la clasificación. Un gráfico de estos puntajes se presenta en la Figura 6.1.
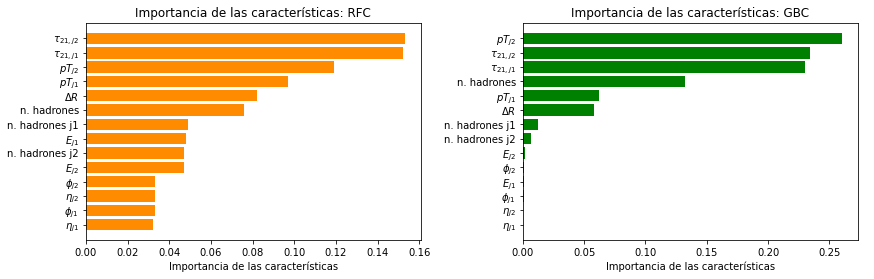
Figura 6.1 Importancia de las variables utilizadas en el entrenamiento realizado con el conjunto de datos R&D según RFC (izquierda) y GBC (derecha).¶
Las características más importantes para ambos clasificadores son la variable de subestructura \(\tau_{21}\), el \(pT\) de los jets y el número de hadrones de los eventos, y las menos importantes son \(\eta\) y \(\phi\). Esto indica que las variables con mayor separación entre las distribuciones de señal y fondo, como se puede ver en la Figura 5.7 del capítulo anterior, son más relevante en el aprendizaje de los modelos.
6.1.1.2. Distribuciones de eventos clasificados¶
Con la clasificación realizada por los distintos modelos, podemos graficar las distribuciones resultantes de los eventos clasificados como señal o fondo y compararlas con las distribuciones de los datos simulados utilizados como entrada. En la Figura 6.2 se encuentran las distribuciones de los datos simulados y de los datos clasificados para las variables más importantes según la Figura 6.1.
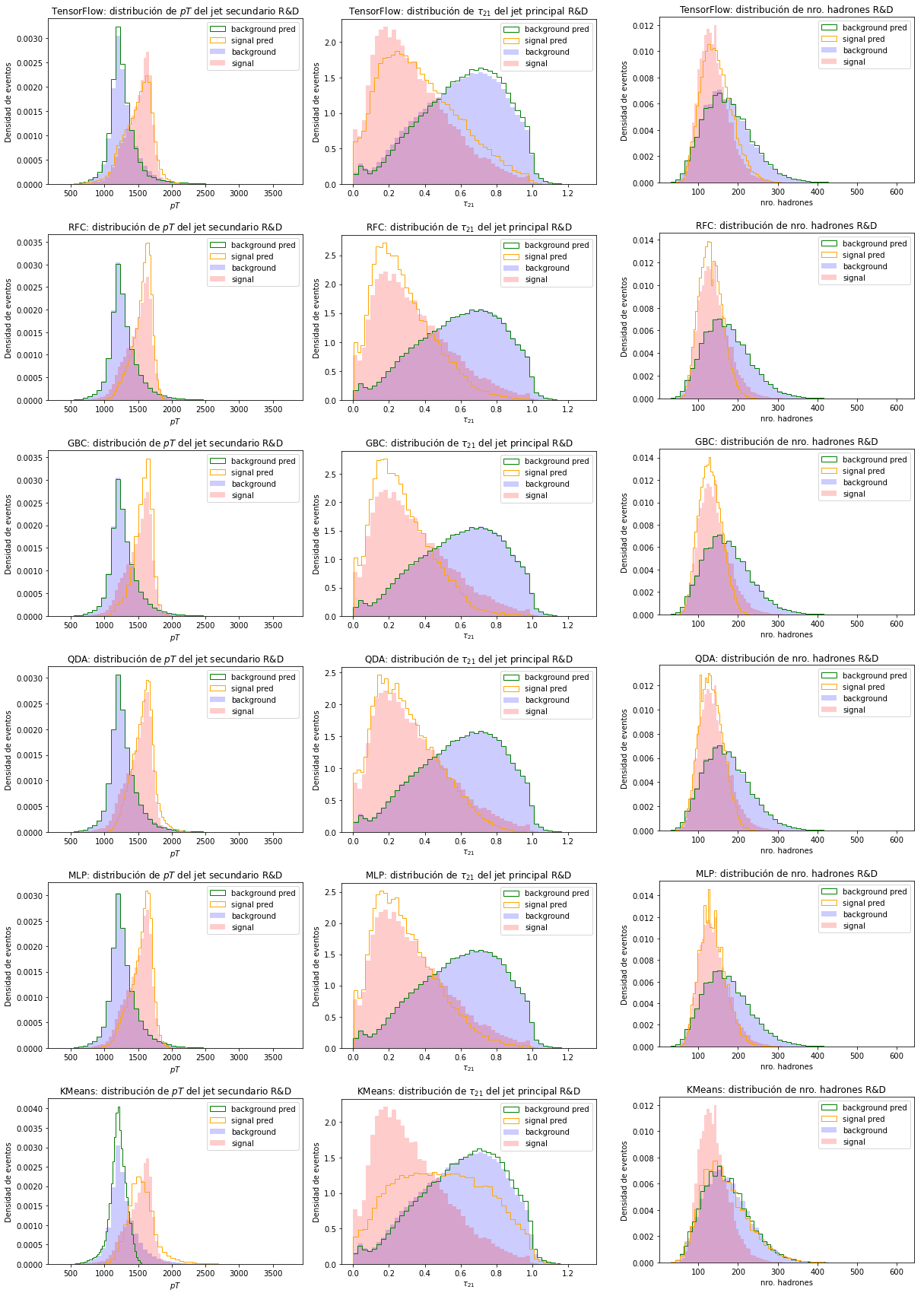
Figura 6.2 Distribución de los datos simulados y la clasificación para algunas de las variables más importantes usando el conjunto prueba R&D. Cada fila de imágenes representa un clasificador. De arriba a abajo: clasificador de TensorFlow, RFC, GBC, QDA, MLP y KMeans. Por columna, de izquierda a derecha, se encuentran las distribuciones de \(p_T\) del jet secundario, \(\tau_{21}\) del jet principal y el número de hadrones de los eventos.¶
En general, las distribuciones obtenidas de la clasificación realizada por los modelos son similare a las de los datos simulados. La distinción entre señal y fondo es lograda de forma más precisa por los modelos supervisados, porque poseen más información sobre los eventos en el momento del aprendizaje, puesto que aprenden utilizando la etiqueta de cada evento.
Particularmente, vemos que el clasificador de Tensorflow está subestimando la cantidad de eventos de señal en todas las variables. Esto se evidencia en los picos de las distribuciones de las variables, donde se observa que las distribuciones de los eventos clasificados como señal poseen menor frecuencia de eventos que la señal simulada utilizada. Al contrario, se observa que RFC, GBC y QDA sobreestiman la cantidad de eventos de señal, puesto que en los picos de señal en cada gráfico se observa que las distribuciones de los eventos clasificados como señal son más frecuentes que los de la señal en las muestras emuladas. El clasificador MLP parece clasificar con mayor precisión, ya que la señal clasificada es más cercana a la simulada. El único modelo no supervisado, Kmeans, logra separar algunos eventos de señal según los gráficos de \(pT\) y de \(\tau_{12}\), pero en el gráfico de número de hadrones vemos que no logra diferenciar entre clases. Esto indica que los eventos de señal predicho están contaminados por eventos de fondo.
Al graficar algunas de las variables con menor importancia según la Figura 6.1, en la Figura 6.3, también se evidencia que el clasificador de TensorFlow está subestimando la cantidad de eventos de señal y que RFC, GBC y QDA sobreestiman la cantidad de eventos de señal. Como se mencionó anteriormente, el modelo MLP clasifica más precisamente, lo que también se observa en estas variables, donde las distribuciones de la clasificación son similares a las de los datos simulados. Para KMeans, se observa nuevamente que los eventos predichos como señal están contaminados por eventos de fondo, puesto que en el gráfico de \(\eta\) el modelo no distingue entre señal y fondo, y en \(\Delta R\) y \(E\) los picos de las distribuciones de los eventos predichos como señal muestran menor frecuencia de eventos que las distribuciones de la señal esperada.
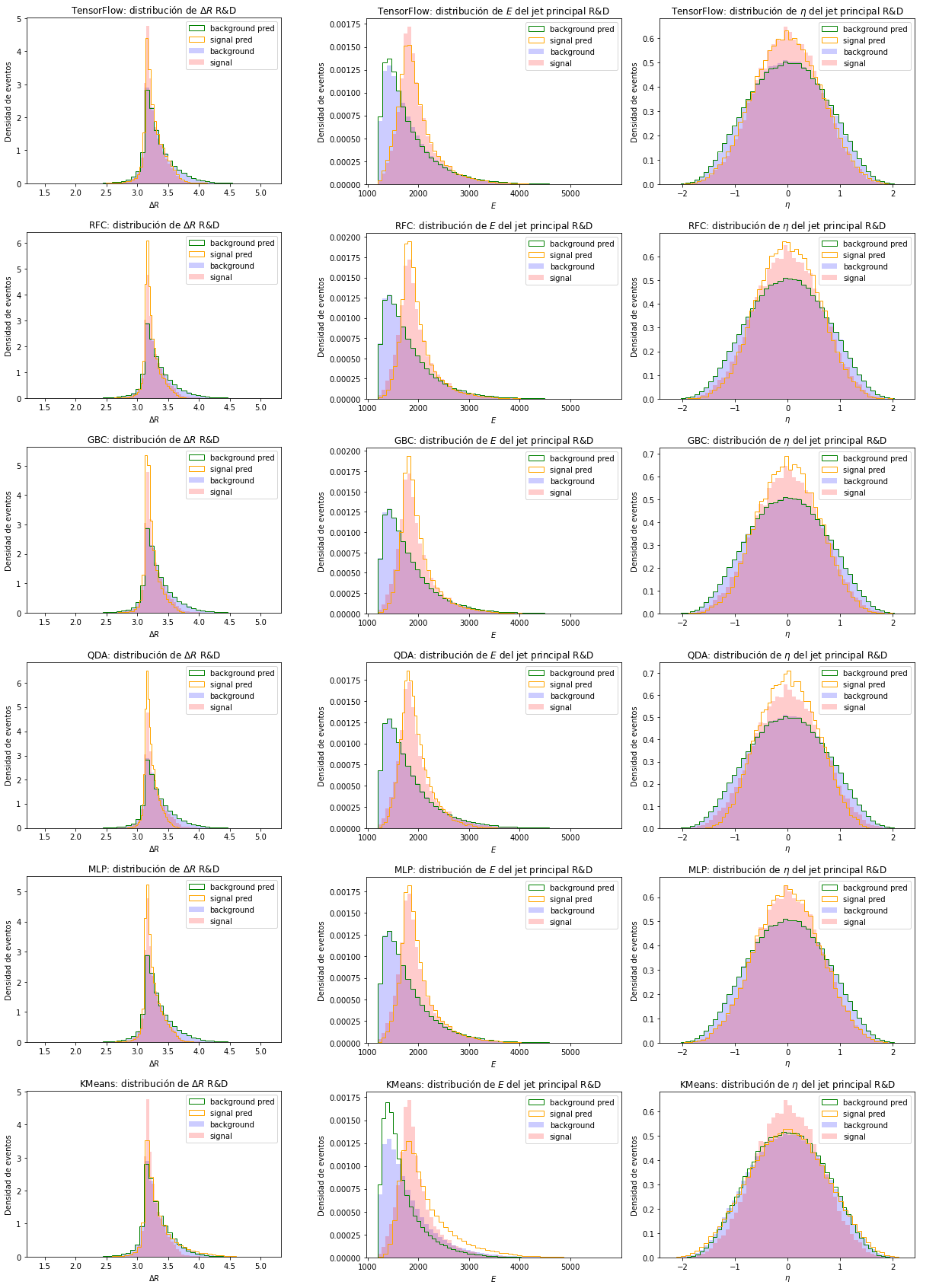
Figura 6.3 Distribución de algunas de las variables menos relevantes para la clasificación. Cada fila de imágenes representa un clasificador. De arriba a abajo: clasificador de TensorFlow, RFC, GBC, QDA, MLP y KMeans. Por columna, de izquierda a derecha, se encuentras las distribuciones de \(\Delta R\), \(E\) del jet principal y \(\eta\) del jet principal.¶
En la Figura 6.4 podemos ver las distribuciones de la variable de masa invariante de acuerdo a la clasificación realizada por los modelos. Las variables de masa son comúnmente utilizadas en la búsqueda de nueva física, pero no fueron utilizadas para el entrenamiento con el objetivo de que los modelos logren búsquedas generales, independientes de las masas de las partículas. En esta variable, se observa que los modelos supervisados obtienen resultados más precisos que el modelo no supervisado.
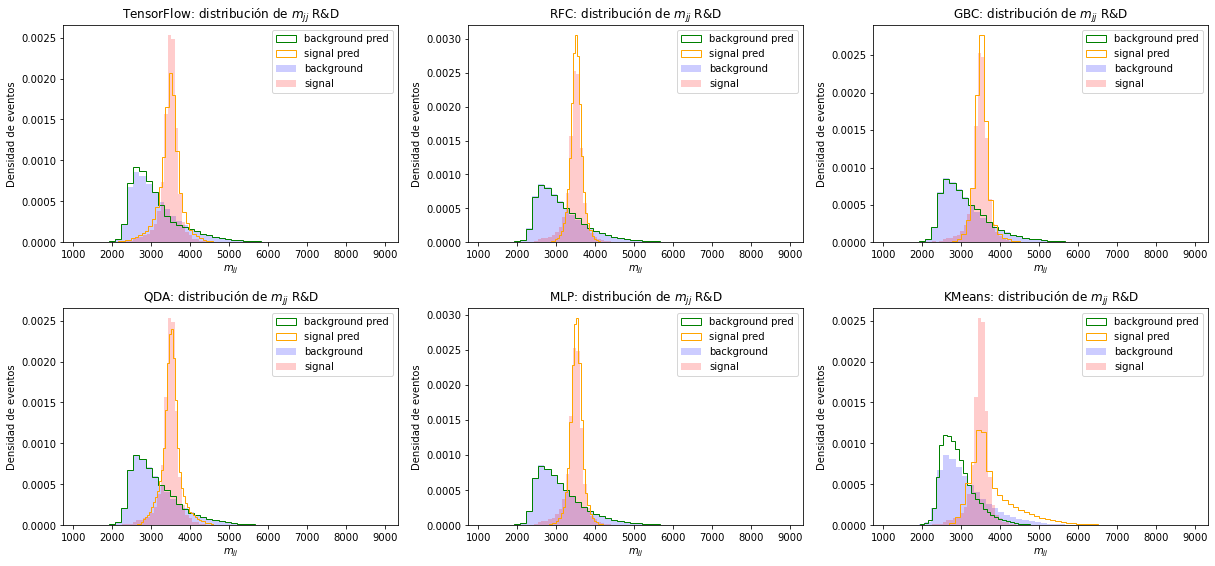
Figura 6.4 Distribución la masa invariante y la clasificación para el conjunto R&D. En la fila superior, de izquierda a derecha, las predicciones de: clasificador de TensorFlow, RFC, GBC y en la fila inferior: QDA, MLP y KMeans.¶
En los modelos supervisados se vuelve a notar lo discutido anteriormente; el modelo de TensorFlow subestima la cantidad de señal y los demás modelos sobreestiman la cantidad de señal. Kmeans obtiene un pico para la señal de magnitud correcta, pero con baja frecuencia, y es evidente que está clasificando eventos de fondo como señal, como se puede notar en el gráfico al observar las distribuciones de señal y fondo entre 4000 y 6000 GeV.
6.1.2. Conjunto BB1¶
El conjunto BB1 se clasifica completamente, utilizando los modelos entrenados con el 70% del conjunto R&D. Como se mencionó en capítulos anteriores, este conjunto posee una menor proporción de señal, 0.08% del conjunto es señal, y las partículas de nueva física son más masivas.
6.1.2.1. Distribuciones de eventos clasificados¶
Las distribuciones de las variables más importantes y la clasificación realizada utilizando el conjunto BB1 se ve en la Figura 6.5.
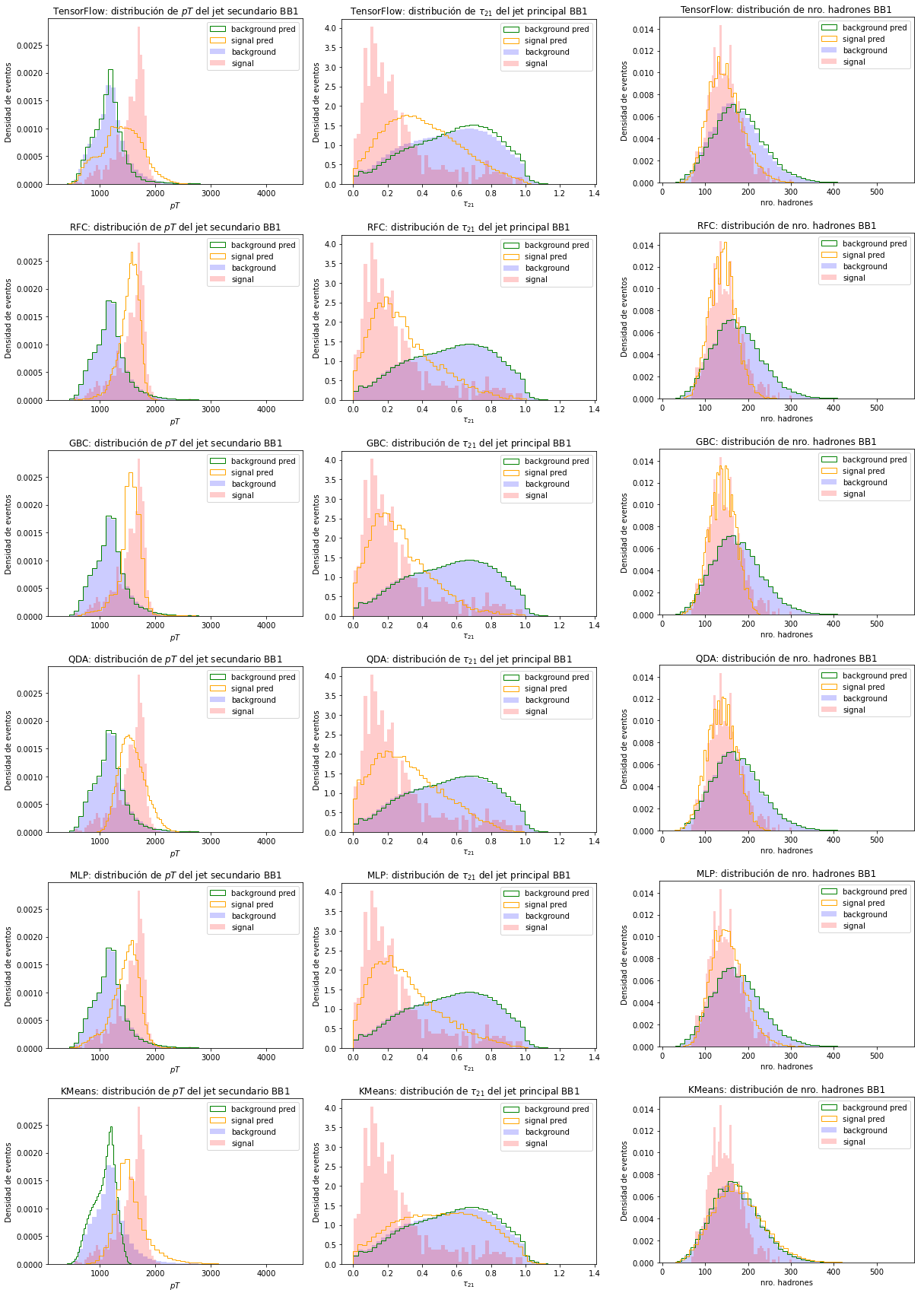
Figura 6.5 Distribución de las variables más importantes y las distribuciones de las clasificaciones para el conjunto BB1. Cada fila de imágenes representa un clasificador. De arriba a abajo: clasificador de TensorFlow, RFC, GBC, QDA, MLP y KMeans. Por columna, de izquierda a derecha, se encuentras las distribuciones de \(pT\) del jet secundario, \(\tau_{21}\) del jet principal y el número de hadrones de los eventos.¶
El poder de distinción entre señal y fondo de los modelos disminuye al utilizar el conjunto BB1, lo que indica que los modelos no logran generalizar del entrenamiento realizado con el conjunto R&D a otro conjunto de datos con masas distintas para las partículas de BSM. A pesar de haber eliminado la masa para el entrenamiento de los modelos, se utilizaron variables que cambian al variar la masa de las partículas de nueva física del evento. Entre estas variables se encuentra el \(pT\) de los jets, que es mayor para los jets del conjunto BB1 debido a que la partícula de nueva física es más masiva, \(\tau_{21}\), debido a que la colisión posee mayor transferencia de momento y las partículas resultantes poseen un mayor impulso, y \(\Delta R\), cuya distribución es más angosta para colisiones más energéticas. Dichas variables se encuentran entre las más importantes para realizar la clasificación, lo que puede afectar la clasificación de datos con distintas masas. La diferencia entre las variables mencionadas anteriormente para la señal en los conjuntos R&D y BB1 se encuentra en la Figura 6.6.
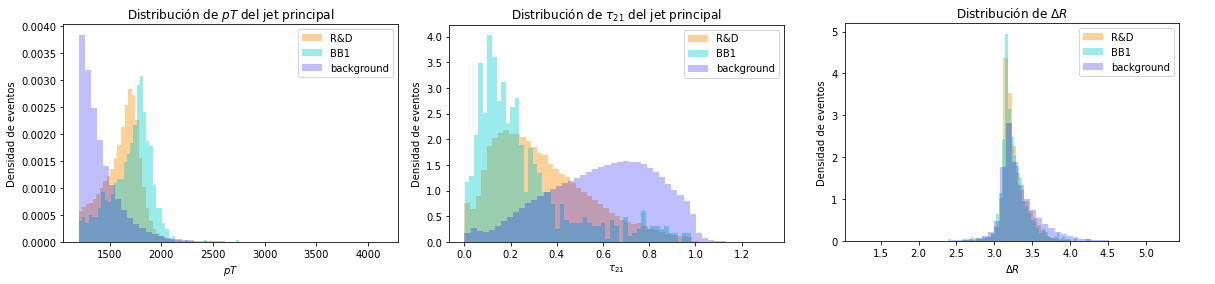
Figura 6.6 Comparación de las distribuciones de señal de las variables \(pT\) del jet principal, \(\tau_{21}\) del jet principal y \(\Delta R\) de los conjuntos de datos R&D y BB1.¶
Los resultados de la clasificación para las variables más relevantes se presentan en la Figura 6.5. A nivel general, se observa que los modelos no logran realizar correctamente la clasificación de eventos de señal y que dicha clasificación se encuentra contaminada por eventos de fondo. En los gráficos de \(pT\), notamos que los modelos obtienen una distribución corrida hacia la izquierda, es decir, aprendieron a clasificar como señal eventos de jets que poseen menor \(pT\). Igualmente en la variable \(\tau_{21}\), si comparamos con la distribución de esta variable en la Figura 6.6, notamos que los modelos están clasificando para una distribución parecida a la del conjunto R&D.
Las distribuciones de las variables menos relevantes para la clasificación se encuentran en la Figura 6.7. Las distribuciones de estas variables refuerzan lo analizado anteriormente. En general, los modelos clasifican señal con un \(\Delta R\) más ancho y jets menos energéticos, similares a las variables del conjunto R&D.
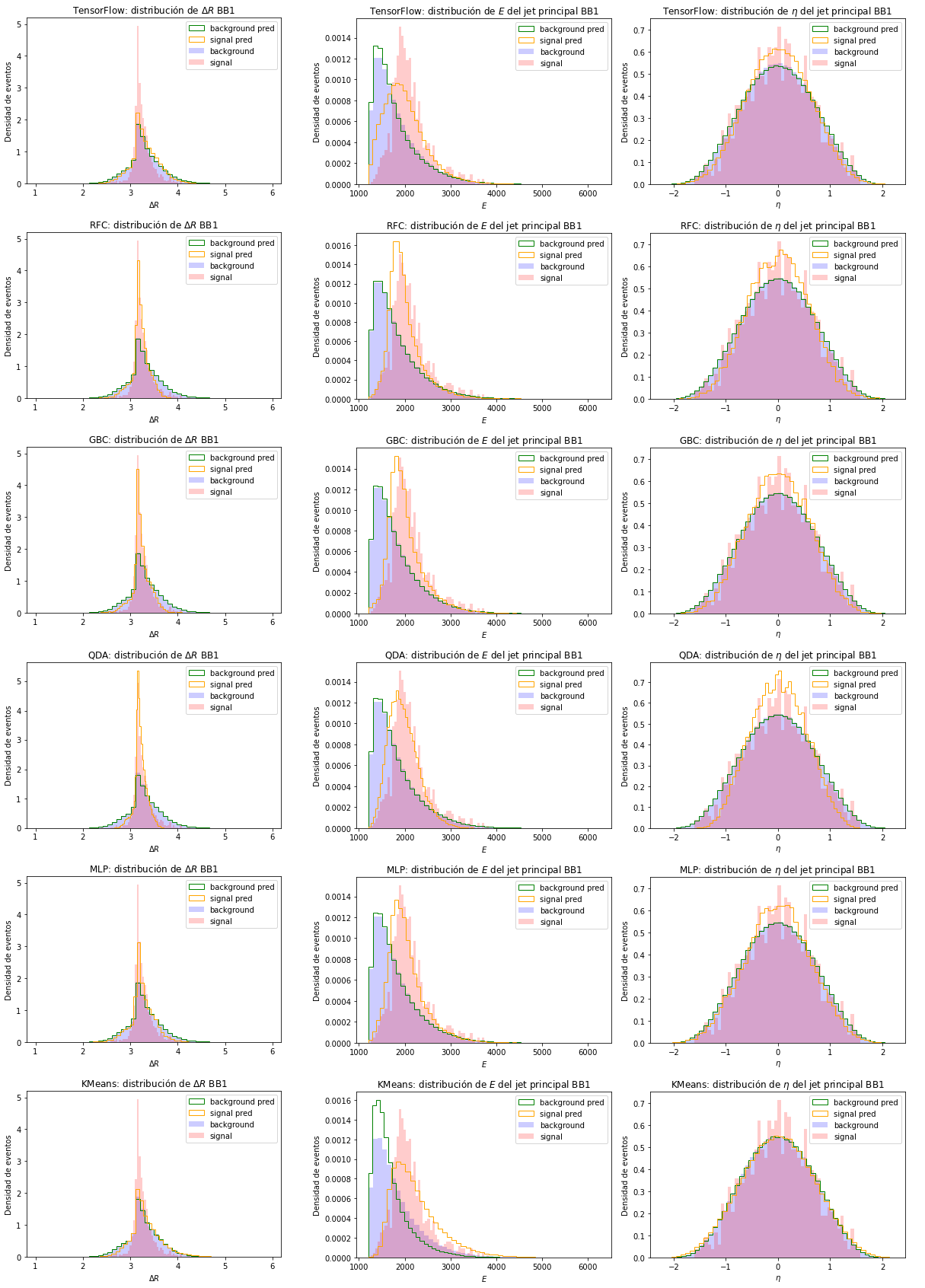
Figura 6.7 Distribución de los eventos simulados y de la clasificación para algunas de las variables menos relevantes del conjunto BB1. Cada fila de imágenes representa un clasificador. De arriba a abajo: clasificador de TensorFlow, RFC, GBC, QDA, MLP y KMeans. Por columna, de izquierda a derecha, se encuentras las distribuciones de \(\Delta R\), \(E\) del jet principal y \(\eta\) del jet principal.¶
Por último, en la Figura 6.8, observamos las distribuciones de masa invariante obtenidas para este conjunto de datos. Ninguno de los modelos reconstruye la distribución de la señal. Particularmente, notamos que los picos de señal están corridos hacia menores valores de masa, indicando que los modelos aprendieron a clasificar eventos con menor masa invariante, como la señal del conjunto R&D, a pesar de no haber utilizado las variables de masa en el entrenamiento y la clasificación.
En todas las variables el clasificador de TensorFlow y KMeans obtienen las distribuciones menos similares a las simuladas. Los demás modelos obtuvieron resultados parecidos entre sí, pero en todos es evidente la contaminación de la clasificación de eventos de señal con fondo y viceversa.
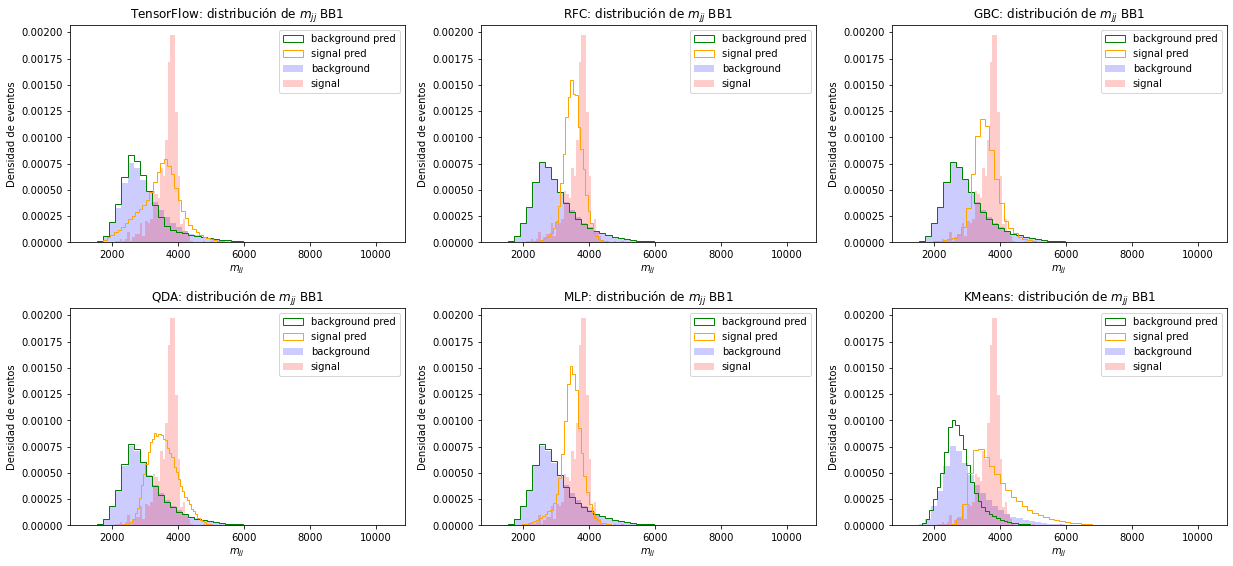
Figura 6.8 Distribución la masa invariante y la clasificación del conjunto BB1. En la fila superior, de izquierda a derecha, las predicciones de: clasificador de TensorFlow, RFC, GBC y en la fila inferior: QDA, MLP y KMeans.¶
Aunque la comparación de distribuciones proporciona un punto de partida para la comparación de los algoritmos, es necesario el uso de métricas (ver Sección 4.4), porque no es evidente cuál algoritmo está logrando una mejor clasificación de los conjuntos de datos.
