Algoritmos para detección de anomalías
Contenido
4.2. Algoritmos para detección de anomalías¶
En este proyecto se trata de resolver un problema de clasificación binaria con los datos de las LHCO 2020, que son altamente desbalanceados. Esto se conoce como una tarea de detección de anomalías, que en el caso de este trabajo hace referencia a la detección de los eventos de señal.
La implementación de aprendizaje automático en este trabajo está comprendida por los siguientes pasos:
Preprocesamiento de los datos utilizando
benchtool, descrito en la Sección 4.5.2.División de los datos en conjuntos mutuamente excluyentes, 70% en un conjunto de entrenamiento y 30% en uno de prueba.
Ajuste de los modelos minimizando una función de pérdida específica para cada uno (ver Sección 3.1.1), utilizando los datos de entrenamiento.
Evaluación del rendimiento del modelo, calculando la función de pérdida con los datos de prueba.
Los algoritmos utilizados en este trabajo se escogieron a partir de su rendimiento, estudiado durante el desarrollo de las herramientas de análisis de datos. Más información sobre cómo se escogieron estos algoritmos se encuentra en la sección notebooks del repositorio de benchtools.
A continuación, se explicarán los algoritmos utilizados, enfocándonos en su uso para la tarea de clasificación binaria. También se resumirán algunos métodos necesarios para explicar más adelante los algoritmos de las LHCO 2020 utilizados en este trabajo. La referencia principal de esta sección es [68].
4.2.1. Bosque aleatorio¶
Los bosques aleatorios son algoritmos supervisados ampliamente utilizados para tareas complejas de clasificación. Estos algoritmos son ensambles de árboles de decisión.
Un árbol de decisión utiliza una serie de preguntas para realizar la partición jerárquica de los datos con el objetivo de hallar un conjunto de reglas que separen el espacio de características[93]. El árbol de decisión utiliza las variables del conjunto de datos para crear preguntas con respuestas booleanas y dividir continuamente el conjunto de datos hasta aislar todos los puntos de datos que pertenecen a cada clase. Este proceso organiza los datos en una estructura de árbol. Cada vez que se hace una pregunta se está agregando un nodo al árbol.
Los árboles de decisión utilizan funciones de pérdida que evalúan la partición de los datos en función de la pureza de los nodos resultantes, una función de pérdida que compara la distribución de clases antes y después de la división[94]. Esto se conoce como criterio de impureza. Uno de los criterios más utilizado es el criterio Gini, que mide cuánto ruido tiene una categoría:
donde \(Q_m\) representa los datos en el nodo \(m\) y \(p_{mk}\) es la proporción de clase \(k\) observada en el nodo \(m\), donde las clases para clasificación binaria son 0 y 1. Un diagrama de un árbol de decisión se observa en la Figura 4.2.
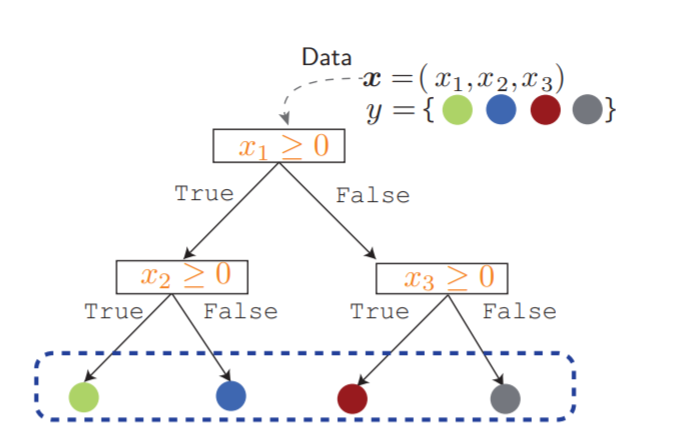
Figura 4.2 Ejemplo de un árbol de decisión. Para una conjunto de características \(\mathbf{x}\), su etiqueta \(y\) es predicha, recorriéndolo desde su raíz, pasando por las hojas, siguiendo las ramas que satisface [68].¶
Para crear un ensamble de árboles de decisión y obtener un bosque aleatorio, se deben utilizar procesos de aleatorización. Usualmente se utilizan en conjunto dos métodos. Los subconjuntos de datos utilizados para entrenar cada árbol se obtienen del conjunto de entrenamiento mediante bootstrapping, un método de muestreo con remplazo. Luego, en la construcción de los árboles de decisión, en cada nodo se utiliza un subconjunto aleatorio de las características de entrada.
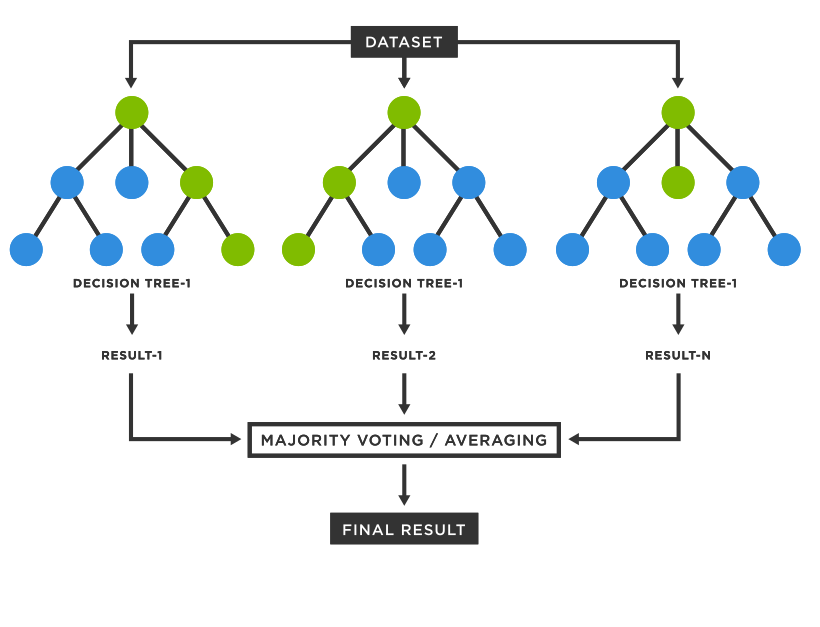
Usualmente, cada árbol emite un voto unitario para la clase más popular dada una entrada y la clase con más votos es asignada a esta entrada[95], como se observa en la Figura 4.3. Sin embargo, la implementación utilizada en este trabajo combina los árboles individuales promediando su predicción probabilística[96].
4.2.2. Potenciación del gradiente¶
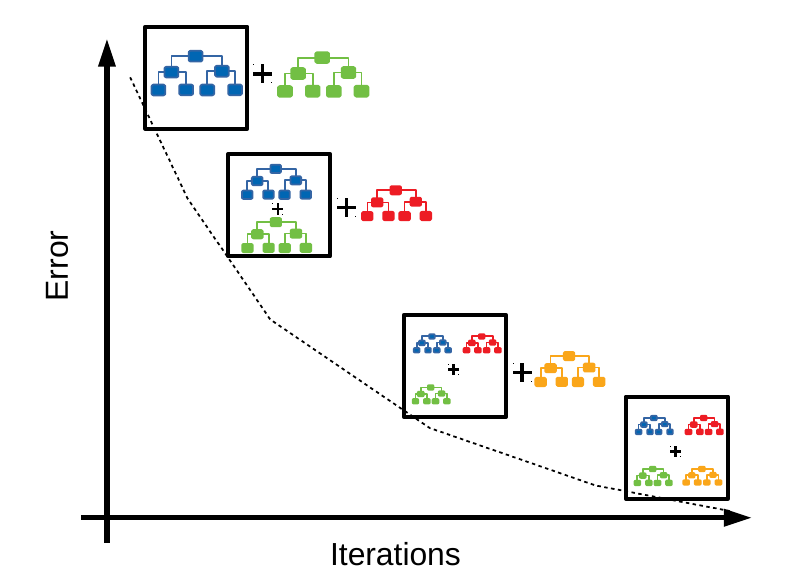
El clasificador de potenciación del gradiente (GBC, por sus siglas en inglés) es un modelo supervisado que utiliza árboles de regresión como aprendiz débil. Es un modelo supervisado y aditivo que avanza por etapas[98]. En cada etapa, se ajusta el árbol al error residual, es decir, el error asociado al árbol anterior, con el objetivo de minimizar el error, como se muestra en la Figura 4.4.
Su formulación matemática es la siguiente[100]: la predicción \(y_i\) del modelo para la entrada \(x_i\) está dada por:
donde \(h_m\) son los aprendices débiles. En el caso de clasificación, el mapeo del valor de \(F_M(x_i)\) a una clase o probabilidad es dependiente de la pérdida. La probabilidad de que \(x_i\) pertenezca a la clase positiva se modela usando la función sigmoide,
El GBC se construye de la siguiente manera:
y \(h_m\) se ajusta para minimizar la suma de las pérdidas dado el ensamble anterior \(F_{m-1}\),
donde \(g_i\) es la derivada de la función de pérdida con respecto a su segundo parámetro, evaluada en \(F_{m-1}(x)\). La suma en la ec.(4.5) se minimiza si \(h(x_i)\) se ajusta para predecir un valor proporcional al gradiente negativo \(−g_i\). Por lo tanto, en cada iteración, el estimador \(h_m\) está ajustado para predecir los gradientes negativos de las muestras. Estos gradientes se actualizan en cada iteración. El proceso puede considerarse como una especie de descenso de gradiente en un espacio funcional.
4.2.3. Análisis de discriminante cuadrático¶
El análisis de discriminante cuadrático (QDA, por sus siglas en inglés)[101] es un clasificador supervisado con un límite de decisión cuadrático. El modelo asume que las densidades condicionales de clase \(P(\mathbf{X}|y=k)\), para cada clase \(k\), están distribuidas normalmente. Las predicciones para cada muestra de entrenamiento \(x\) se obtienen utilizando el teorema de Bayes:
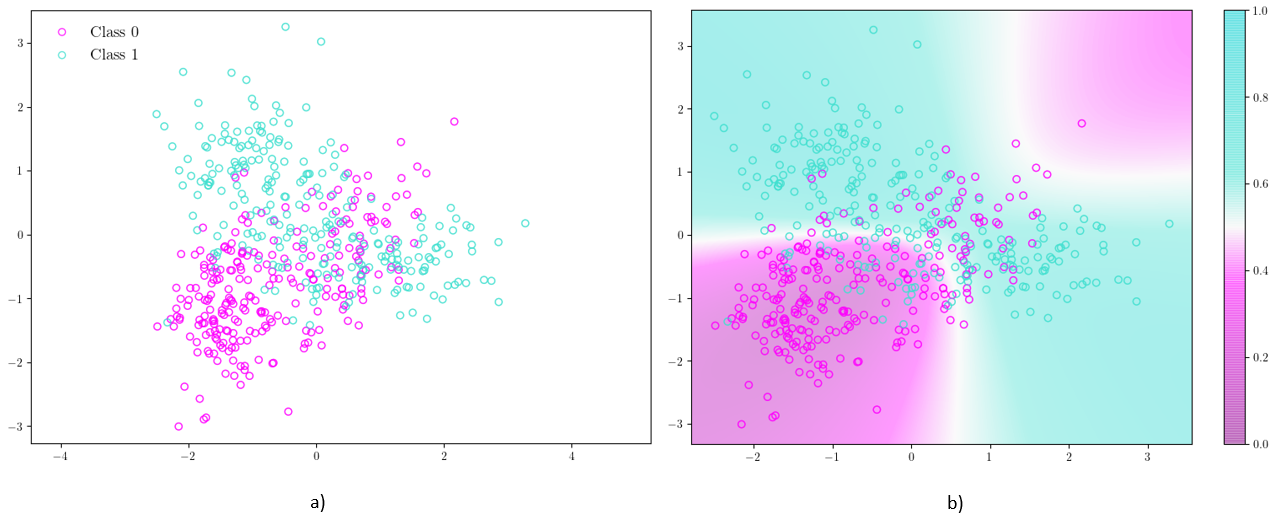
donde se selecciona la clase \(k\) que maximice esta probabilidad. Un ejemplo de clasificación utilizando este método se observa en la Figura 4.5.
4.2.4. Redes neuronales¶
Las redes neuronales (NN, por sus siglas en inglés) son modelos supervisados y no lineales inspirados en las neuronas. Se definen mediante una serie de transformaciones que mapean la entrada \(x\) a estados «ocultos» \(\mathbf{h}_i\). Finalmente, una última transformación mapea estos estados a una función de salida \(\mathbf{y}\)[64]. Esto también se conoce como perceptrón multicapas. Las transformaciones se pueden escribir matemáticamente como:
donde \(g_i\) es una función conocida como función de activación y \(\mathbf{h}_i\) representa la transformación iésima de \(\mathbf{x}\), llamada encaje. \(W\) es la matriz de los pesos y \(\mathbf{b}\) el vector de los sesgos.
El objetivo es hallar los pesos y sesgos que optimizan la función de pérdida. Esto se logra utilizando las etiquetas de los datos y calculando el gradiente de la función de pérdida con respecto a los parámetros del modelo. Este proceso se conoce como retropropagación y requiere que las funciones sean diferenciables.
Las transformaciones se ordenan en capas, como se observa en la Figura 4.6, donde la salida de una capa es la entrada de la siguiente.
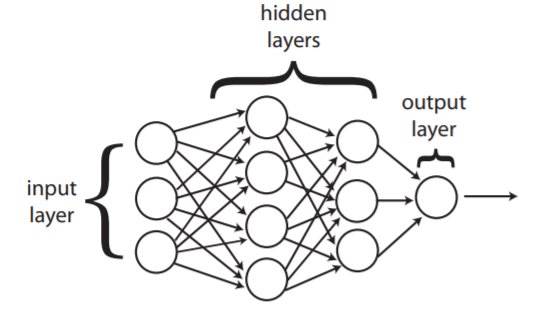
Figura 4.6 Diagrama de una red neuronal. Las transformaciones se ordenan por capas, donde la salida de una capa es la entrada de la siguiente[68]¶
La tarea de la red depende de su arquitectura. Aunque su uso es extenso, nos enfocaremos en su aplicación para clasificación binaria. Para utilizar una red neuronal como clasificador binario, se utiliza la función sigmoide como función de activación de la última transformación. Se suele utilizar la entropía cruzada binaria como función de pérdida, que calcula la entropía cruzada entre las clases predichas y las clases reales.
donde \(N\) es el número de muestras a clasificar, \(y_i\) es la etiqueta de la muestra iésima y \(p(y_i)\) es la probabilidad de que la muestra sea de clase 1.
4.2.5. K-means¶
K-means es un algoritmo no supervisado que separa los datos en \(K\) grupos con igual varianza. Los grupos están caracterizados por la media de los datos pertenecientes al grupo. Estos se conocen como «centroides» y se representan con \(\mu_k\)[103].
El objetivo del algoritmo es minimizar la inercia o criterio de suma de cuadrados dentro del grupo, definida como:
donde \(\mathbf{x}_n\) es la observación enésima y \(r_{nk}\) es la asignación. \(r_{nk}\) es 1 si \(x_n\) pertenece al grupo y 0 de otra forma.
El algoritmo funciona mediante los siguientes pasos:
Algorithm 4.1 (K-means)
Escoger los centroides. En la primera inicialización se escogen puntos aleatorios de los datos.
Asignar cada muestra al centroide más cercano, minimizando \(\mathcal{C}\).
Crear nuevos centroides tomando el valor medio de todas las muestras asignadas a cada centroide anterior.
Calcular la diferencia entre los centroides anteriores y los nuevos.
Los últimos tres pasos se repiten hasta que la diferencia entre los centroides esté debajo de un umbral, es decir, hasta que los centroides no se muevan significativamente. Como la inicialización de los centroides es aleatoria, usualmente se realizan múltiples inicializaciones y se escoge la que resulte en un menor valor de la inercia.
4.2.6. Codificador automático¶
Los codificadores automáticos (AE, por sus siglas en inglés) son redes neuronales de aprendizaje no supervisado que mapean una entrada a una representación comprimida en un encaje, o espacio latente, y luego vuelve a sí misma, como se representa en la Figura 4.7. Al aprender como reproducir la salida original, el modelo extrae características de los datos de entrada[104].
Estas redes se pueden dividir en dos partes. El codificador, que comprime los datos a un espacio latente, y el decodificador que produce la reconstrucción[105]. Una medida de qué tan bien funciona el codificador es la diferencia entre la entrada y la salida de acuerdo a alguna métrica de distancia conocida como «error de reconstrucción».
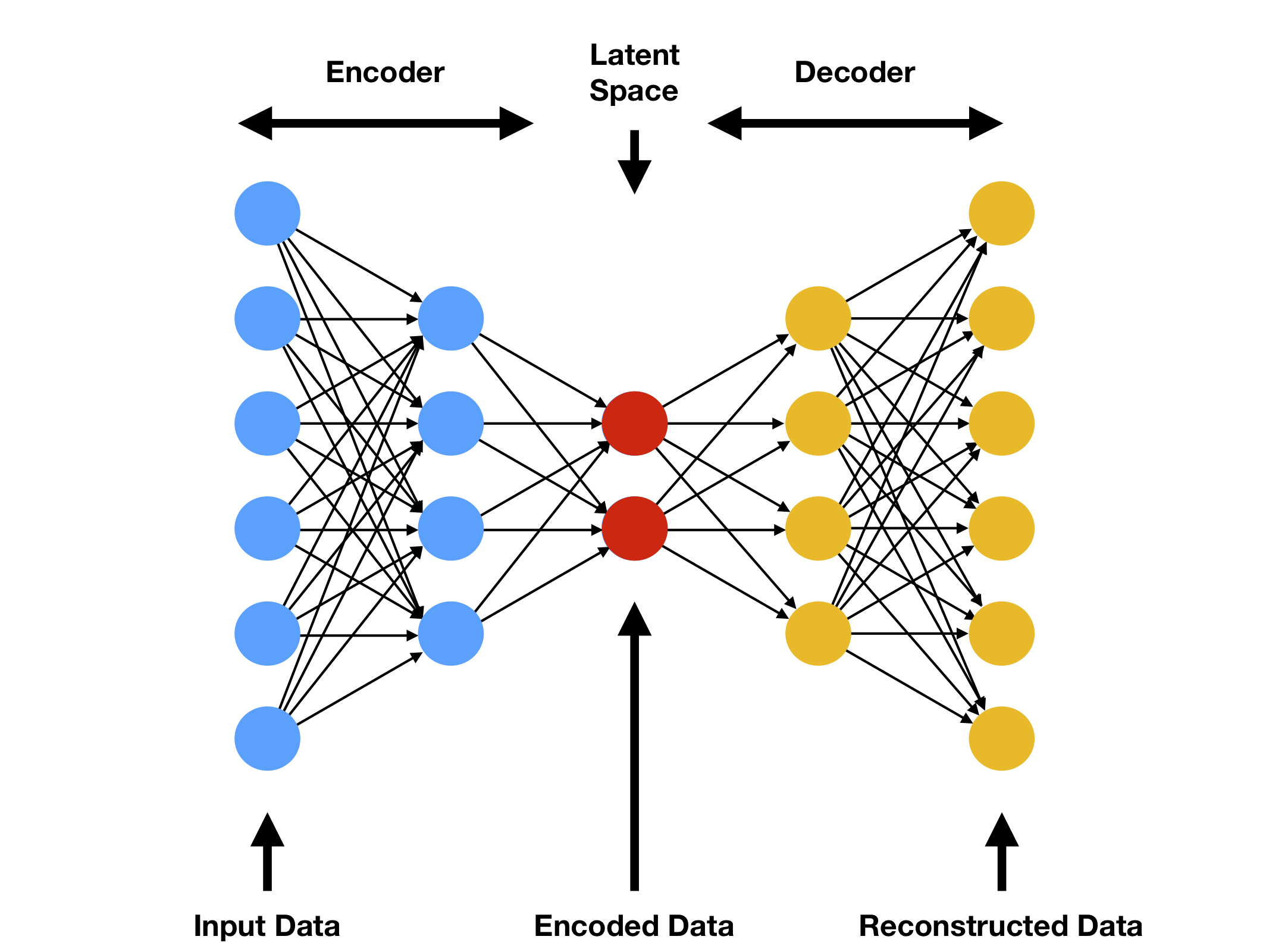
Figura 4.7 Diagrama del funcionamiento de un codificador automático. La entrada se mapea a una representación de dimensionalidad reducida y luego es reconstruida [106].¶
Este algoritmo se ha empezado a utilizar en HEP como detector de anomalías puesto que, al entrenar el codificador automático en una muestra de eventos de fondo, va a aprender las características de fondo, y se espera que un evento de señal no sea reconstruido correctamente. Así, se puede utilizar un corte en el error de reconstrucción como un umbral de anomalía[106].
4.2.7. Red generativa antagónica¶
Una red generativa antagónica (GAN, por sus siglas en inglés) está basada en modelado generativo y en conceptos de teoría de juegos.
El modelado generativo es una tarea de aprendizaje no supervisado en la que los modelos aprenden automáticamente regularidades o patrones en los datos de entrada, con el objetivo de generar nuevos ejemplos que podrían haberse extraído del conjunto de datos original.
Una GAN se construye a partir de dos redes neuronales conocidas como generador y discriminador. El generador aproxima una función generadora \(G(z)\),
donde \(\mathbf{z}\) es muestreado a partir de una distribución de probabilidad a priori en un espacio latente y \(\mathbf{\hat{x}}\) son las muestras generadas. El discriminador aproxima una función discriminadora que distingue entre muestras \(\mathbf{x}\) de los datos originales y muestras \(\mathbf{\hat{x}}\) sintéticas.
El discriminador se entrena para diferenciar entre las muestras sintéticas y los datos reales y el generador para engañar al discriminador. La función de pérdida del discriminador depende de los parámetros del generador y viceversa. Los modelos se entrenan juntos hasta que el discriminador es engañado una cantidad de veces sobre algún umbral, lo que significa que el generador está generando ejemplos plausibles.