Métricas de rendimiento
Contenido
4.4. Métricas de rendimiento¶
La clasificación es una de las tareas más comunes en el aprendizaje automático. Sin embargo, no existe un algoritmo que funcione mejor para todos los problemas; cada algoritmo tiene ventajas y desventajas. Por lo tanto, requerimos formas de medir el grado en que la clasificación obtenida con un algoritmo y las etiquetas reales de los datos coinciden. Un resumen de las métricas más comunes para la tarea de clasificación binaria, y las utilizadas en este trabajo, se presenta a continuación.
4.4.1. Métricas numéricas¶
La métrica de evaluación primaria es la matriz de confusión. En esta matriz se resumen el número de etiquetas predichas correctamente e incorrectamente.

Figura 4.9 Matriz de confusión. El texto en azul representa los nombres utilizados en HEP.¶
La diagonal en la matriz de confusión, como se observa en Figura 4.9, representa las etiquetas predichas correctamente, mientras que los elementos fuera de la diagonal son las predicciones incorrectas. A partir de los valores de esta matriz se definen el resto de las métricas.
En la Tabla 4.3 se presenta un resumen de las métricas numéricas utilizadas comúnmente para clasificación binaria[110].
Métrica |
Ecuación |
Enfoque de evaluación |
|---|---|---|
Exactitud |
\(\frac{TP+TN}{TP+FP+FN+TN}\) |
Número correcto de predicciones sobre todas las predicciones hechas |
Precisión |
\(\frac{TP}{TP+FP}\) |
Proporción de tasa de verdaderos positivos |
Recuperación |
\(\frac{TP}{TP+FN}\) |
Efectividad del clasificador para identificar etiquetas positivas |
Especificidad |
\(\frac{TN}{TN+FP}\) |
Efectividad del clasificador para identificar etiquetas negativas |
Puntaje f1 |
\(\frac{(\beta^2+1)TP}{(\beta^2+1)TP+\beta^2FN+FP}\) |
Promedio ponderado de precisión y sensibilidad |
El nombre de las métricas varía en distintas áreas. En HEP, la recuperación y especificidad se conocen como eficiencia de señal (\(\epsilon_s\)) y rechazo de fondo (\(1-\epsilon_{b}\)), respectivamente. La precisión se conoce como pureza (\(\rho\))[111].
Las métricas utilizadas dependen del problema de clasificación. Para datos altamente desbalanceados, es decir, datos con una desproporción significativa entre el número de ejemplos de cada clase, se descarta la exactitud ya que puede resultar en valores altos a pesar de estar prediciendo incorrectamente la etiqueta para la clase minoritaria. Alternativamente, se puede usar la exactitud balanceada:
En este trabajo se utilizan las métricas descritas en la Tabla 4.3, salvo la exactitud, que se sustituye por la exactitud balanceada, y la especificidad.
4.4.2. Métricas bidimensionales¶
Las métricas bidimensionales más conocidas son la curva característica de funcionamiento del receptor (curva ROC, por sus siglas en inglés) y la curva precisión-recuperación (curva PR).
4.4.2.1. Curva ROC¶
Los clasificadores usualmente asignan un puntaje \(\mathcal{D}\) de manera que una puntuación más alta significa mayor probabilidad de ser señal. La clasificación discreta se logra escogiendo un punto de operación, es decir, escogiendo un umbral de decisión \(\mathcal{D}_{thr}\), de manera que todas las muestras que cumplan \(\mathcal{D}\geq\mathcal{D}_{thr}\) se clasifican como positivas, o señal, y todas las demás como negativas, o fondo[112].
La curva ROC se construye graficando la recuperación vs. 1-especificidad para varios umbrales de decisión. En términos de HEP, la eficiencia de señal vs. la eficiencia de fondo. Una ilustración de estas curvas se observa en la Figura 4.10.
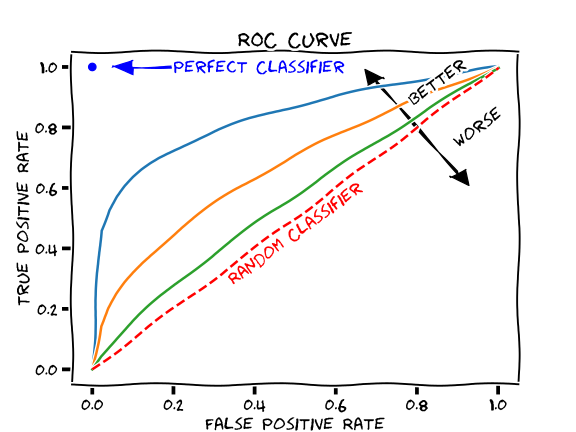
Figura 4.10 Ilustración de la curva ROC. La diagonal representa a un clasificador aleatorio o que no distingue entre clases. En este caso, el clasificador con la curva azul es mejor distinguiendo entre clases[113].¶
El área bajo de la curva (AUC, por sus siglas en inglés) representa la habilidad del clasificador para distinguir entre clases,
Un valor de AUC de 0.5 indica que la predicción no es mejor que una clasificación aleatoria. Menor a 0.5 indica que el clasificador está clasificando de manera inversa[114].
Los clasificadores de agrupamiento, como K-Means, no asignan puntuaciones relacionadas a la probabilidad de ser señal. Sin embargo, asignan distancias entre los datos, representados como puntos, y los centroides. En este trabajo, se tomó la distancia hacia el centroide de señal como el puntaje relacionado a la probabilidad de ser señal, de manera que los puntos más cercanos al centroide de señal poseen un puntaje mayor que los puntos más lejanos. Esta consideración se realizó para la curva ROC y las demás métricas bidimensionales.
En HEP se utilizan versiones de esta curva. Es común graficar eficiencia de señal vs. rechazo de fondo, en vez de la curva ROC clásica, y el AUC se calcula en términos de estas variables. También se suele graficar el inverso de la eficiencia de fondo vs. eficiencia de señal. Ejemplos de ambas curvas se observan en la Figura 4.11.
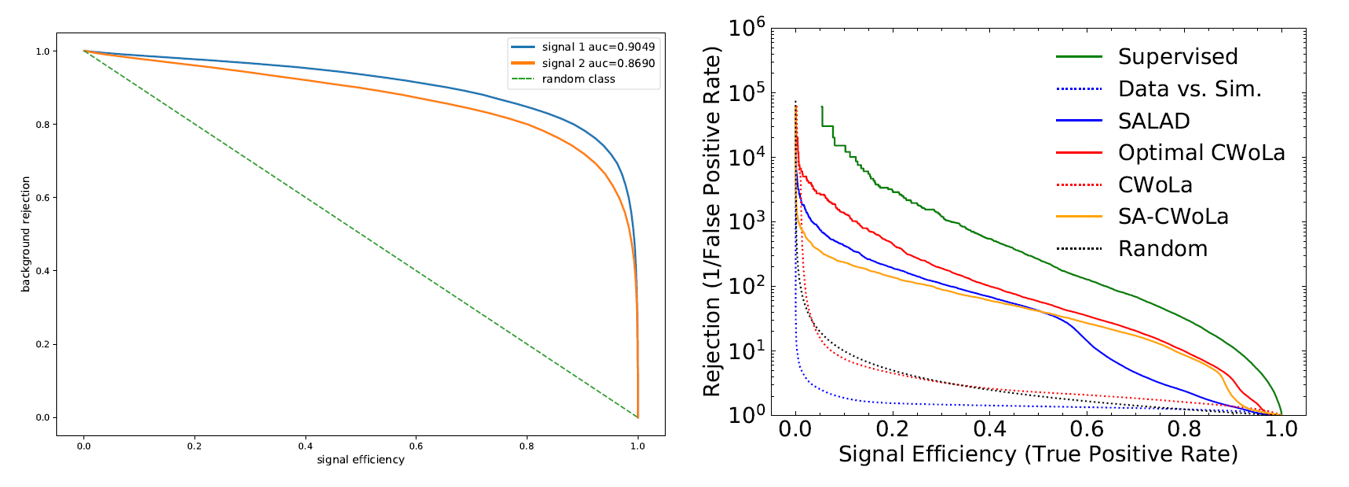
Figura 4.11 Ejemplos de otras versiones de la curva ROC. A la izquierda la curvas de eficiencia de señal vs. rechazo de fondo. A la derecha, inverso de la eficiencia de fondo vs. eficiencia de señal[75].¶
La curva ROC y el AUC tienen sus limitaciones[112]:
La comparación de dos curvas ROC que se cruzan no es tan evidente, ya que el AUC se construye como una integral que otorga el mismo peso a todas las partes de la curva. Sin embargo, para la clasificación se escoge un punto específico. En este caso, otras métricas se deben utilizar para definir cuál clasificador proporciona mejor rendimiento en la región donde se elija el umbral de decisión.
El uso de las curvas ROC puede no ser apropiado para problemas que incluyan datos altamente desbalanceados, debido a que conduce a evaluaciones demasiado optimistas. La curva PR puede ser más informativa en este caso.
4.4.2.2. Curva PR¶
Para datos altamente desbalanceados se suele sugerir el uso de la curva PR:
Si la proporción de instancias positivas y negativas en un conjunto de prueba cambia, la curva ROC no cambia. […]Métricas como la exactitud, la precisión, las curvas de aumento y el puntaje F usan valores de ambas columnas de la matriz de confusión. Cuando la distribución de clases cambia, estas métricas también cambian, incluso si el rendimiento del clasificador no cambia. Las curvas ROC se basan en la tasa de TP y FP, en la cual cada dimensión es una proporción de la columna, por lo que no depende de la distribución de clases.
— ROC Graphs: Notes and Practical Considerations for Data Mining Researchers, 2003[115].
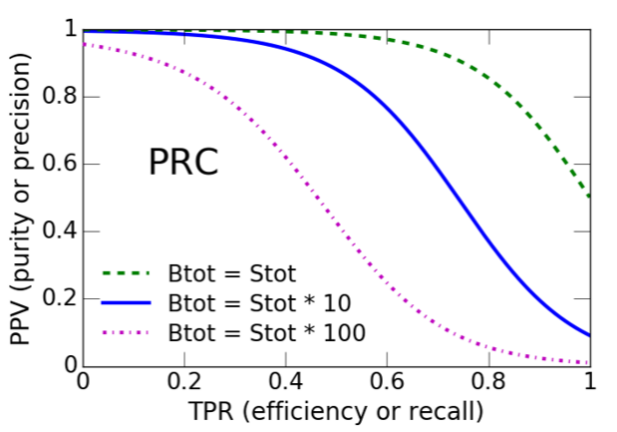
Para obtenerla, se grafica la precisión vs. la recuperación, como se observa en la Figura 4.12.
Análogo al AUC, se utiliza el área bajo la curva PR (AUCPR, por sus siglas en inglés) y la precisión promedio (AP, por sus siglas en inglés). La precisión promedio resume la curva PR utilizando la media ponderada de las precisiones logradas en cada umbral, usando como peso el aumento en recuperación del umbral anterior[116].
donde \(P_n\) y \(R_n\) son la precisión y la recuperación del umbral enésimo.
4.4.2.3. Mejora de la significancia¶
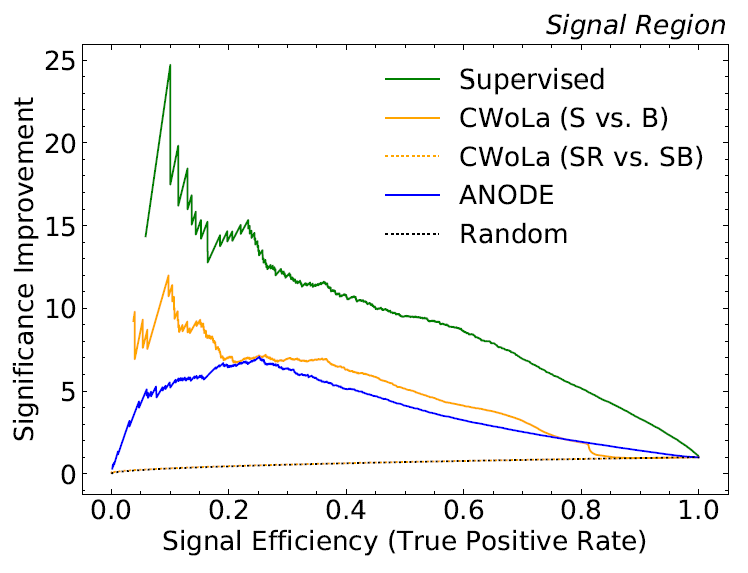
Otra medida utilizada regularmente en HEP es la mejora de la significancia, definida como:
Una mejora de la significancia igual a 2 significa que la mejora de la significancia inicial es amplificada por un factor de 2 después de utilizar la estrategia de clasificación[75].
Así, se grafica la mejora de la significancia vs. eficiencia de señal con el fin de visualizar la mejora de la significancia del clasificador en múltiples umbrales. Un ejemplo de esta curva se observa en la Figura 4.13.