Reconstrucción de jets
Contenido
2.5. Reconstrucción de jets¶
Como se explicó en la Sección 2.2.3, la formación de un jet resulta en múltiples partículas de color neutro. Las características de estas partículas del estado final es lo que se mide en los detectores, es decir, es la información que se obtiene de los jets. Por lo tanto, para analizar los eventos de jets es necesario reconstruirlos. En esta sección se explicarán los algoritmos más conocidos para reconstruirlos y algunas de las variables que se utilizan para caracterizarlos.
2.5.1. Agrupamiento de jets¶
La definición de un jet no es única. De hecho, la existencia de un jet es dependiente de la regla matemática que lo define. Esta regla matemática agrupa los constituyentes del jet de acuerdo a propiedades cinemáticas y se conoce como algoritmo de agrupamiento de jets. A continuación, se explicará acerca de estos algoritmos siguiendo[20, 48, 52].
De manera general, un algoritmo de agrupamiento hace un mapeo del conjunto de hadrones del estado final con cuadrimomento \(\{p_1^{had},p_2^{had},\dots,p_n^{had}\}\) a un conjunto de jets con cuadrimomento \(\{p_1^{jet},p_2^{jet},\dots,p_m^{jet}\}\), donde \(m<n\). El momento de cada jet es la suma de los momentos de las partículas que lo constituyen y la suma vectorial define el eje del jet.
Todos los algoritmos agrupan objetos cercanos en \(\phi\), el ángulo azimutal alrededor del eje del haz, y la pseudorapidez \(\eta\), definida como:
donde \(\theta\) es el ángulo polar entre los constituyentes y el haz de protones entrantes. Los valores de pseudorapidez indican directamente a qué distancia del centro del detector se produce una partícula y varían de menos a más infinito dentro de la geometría del detector. Este sistema de coordenadas del detector se muestra en la Figura 2.13, junto con la conversión de ángulo polar a pseudorapidez.
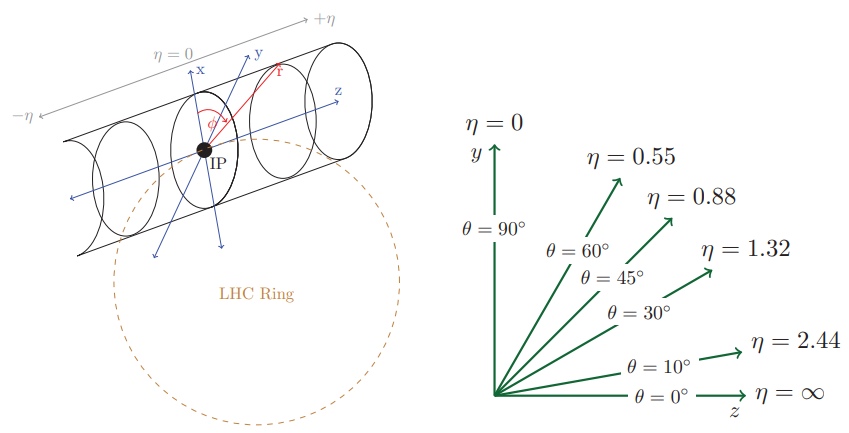
Figura 2.13 Ilustración del sistema de coordenadas utilizado en los experimentos del LHC (izquierda) y una conversión entre el ángulo polar y la pseudorapidez (derecha). El eje z se encuentra a lo largo de la dirección del haz de protones entrante, y el ángulo azimutal \(\phi\) se define con respecto al plano x–y, como es usual. La pseudorapidez \(\eta\) se define para aprovechar la simetría cilíndrica, y aumenta de valor a medida que nos alejamos del centro del detector[20].¶
La distancia angular entre dos objetos en el detector está dada en función de \(\eta\) y \(\phi\),
Los jets se pueden reconstruir a partir de objetos experimentales, como depósitos de energía en calorímetros y trayectorias de partículas cargadas (Figura 2.14), o de objetos teóricos, como partones y hadrones obtenidos mediante simulaciones.
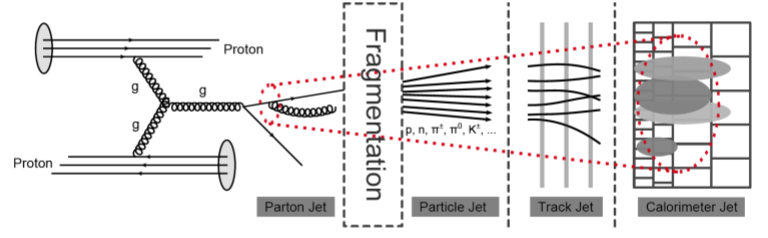
Figura 2.14 Esquema que muestra los diferentes tipos de jet. Se producen partículas de color por la dispersión fuerte, creando partículas de color neutro en la fragmentación. Estas partículas pueden producir distintas señales en los detectores[6].¶
Se espera que un algoritmo posea ciertas características:
Ser robusto con respecto al tipo de datos de entrada.
Teóricamente, debe ser colinealmente estable: la separación de un partón en dos partones colineales no debe cambiar el resultado del agrupamiento del jet (Figura 2.15).
Cumplir con la estabilidad infrarroja: la radiación de un gluon suave no debe cambiar el agrupamiento (Figura 2.16).
Baja sensibilidad a los UE y el pileup (PU, por sus siglas en inglés), que son señales remanentes de otras colisiones.
Fácil de utilizar en cálculos teóricos y análisis experimentales, así como computacionalmente rápidos de ejecutar.
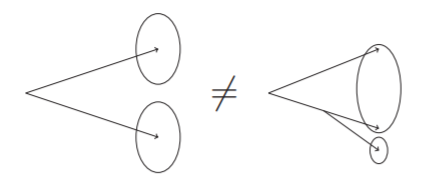
Figura 2.15 Esquema de la estabilidad colineal. La separación de un partón en partones colineales no debe cambiar la configuración de un jet[48].¶
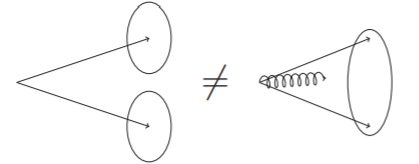
Figura 2.16 Esquema de la estabilidad infrarroja. La emisión de un gluon suave entre dos jets no debe resultar en su unión[48].¶
2.5.1.1. Tipos de algoritmos¶
Existen dos tipos principales de algoritmos de agrupamiento: algoritmos de cono y algoritmos de recombinación secuencial
2.5.1.1.1. Algoritmos de cono¶
Los algoritmos de cono asumen que el jet se encuentra en regiones cónicas del espacio \((\eta-\phi)\), por lo que los jets reconstruidos por estos algoritmos tienen bordes circulares. Son de fácil implementación, pero no son colinealmente estables[53].
Se puede pensar que su aproximación es de arriba hacia abajo. En general, un algoritmo de cono sigue los pasos a continuación[54]:
Algorithm 2.1 (Algoritmo de cono)
Inputs Constituyentes del evento
Hallar el constituyente más energético del evento, o semilla.
Colocar un cono de radio R alrededor de esta semilla y sumar el momento de todas las partículas que constituyen el cono, formando un jet de prueba.
Comparar el eje de la semilla con el del jet de prueba:
Si el eje del del jet de prueba y la semilla coinciden: El jet de prueba se toma como jet
De otra forma: Se repiten los pasos anteriores con el eje del jet de prueba como semilla.
Estos pasos se repiten hasta que no haya semillas sobre un umbral de energía escogido.
Ejemplos de algoritmos de cono son: Midpoint Cone, utilizado en Tevatron, Iterative Cone y SISCone[55].
2.5.1.1.2. Recombinación secuencial¶
Los algoritmos de recombinación secuencial asumen que los constituyentes de un jet poseen una pequeña diferencia en el momento transverso. Por esto, las partículas son agrupadas en el espacio de momento, resultando en jets con fluctuaciones en el espacio \((\eta-\phi)\)[53].
En general, los algoritmos de recombinación secuencial utilizan las siguientes medidas de distancia entre dos constituyentes:
donde \(p_T\) es el momento transverso de las partículas, \(\Delta R_{ij} = \sqrt{(\eta_i-\eta_j)^2+(\phi_i-\phi_j)^2}\) es la distancia entre dos constituyentes en el espacio \((\eta-\phi)\), \(R\) es el radio final del jet, usualmente entre 0.4-0.7 y \(p\) es un parámetro referente al tipo de algoritmo.
También utilizan la distancia entre el eje del haz y el constituyente detectado:
Se puede pensar que el funcionamiento de estos algoritmos es de abajo hacia arriba:
Algorithm 2.2 (Algoritmo de recombinación secuencial)
Inputs Constituyentes del evento
Hallar el mínimo en el conjunto \(\{d_{ij},d_{iB}\}\):
Si el mínimo es \(d_{ij}\): los constituyentes i y j se unen en un solo constituyente ij, sumando el cuadri-momento y eliminando i y j de la lista de constituyentes.
Si el mínimo es \(d_{iB}\): i se considera jet y eliminado de la lista de constituyentes.
Los pasos anteriores se repiten hasta que todas las partículas son parte de un jet, con distancias \(\Delta R_{ij}\) entre los ejes de los jets mayores a \(R\) (agrupamiento inclusivo), o hasta que se obtenga una cantidad específica de jets (agrupamiento exclusivo).
Los algoritmos de recombinación utilizados son:
Kt[56]: para este algoritmo \(p=1\). Es sensible a los UE y PU. Este algoritmo es una aproximación inversa del proceso de ramificación de QCD porque preserva la historia de agrupamiento.
Anti-kt[57]: para este algoritmo \(p=-1\). Contrario al kt, es poco sensible a los UE y el PU. En este algoritmo el agrupamiento no está relacionada a la manera en la que los partones se dividen.
Cambridge/Aachen[58]: para este algoritmo \(p=0\). Es el mejor para estudiar la subestructura de los jets, pero su implementación es más complicada. También es susceptible a los UE y el PU.
Los algoritmos de recombinación son los más utilizados en la actualidad desde su implementación en el programa FastJet[59], un paquete de C++ que proporciona herramientas para agrupar y analizar jets. En este trabajo se agrupan los jets utilizando el algoritmo anti-kt.
2.5.2. Variables de subestructura¶
La subestructura de un jet puede analizarse para diferenciar si el jet proviene de un gluon, un quark, un bosón que decae hadrónicamente o partículas masivas aún no descubiertas.
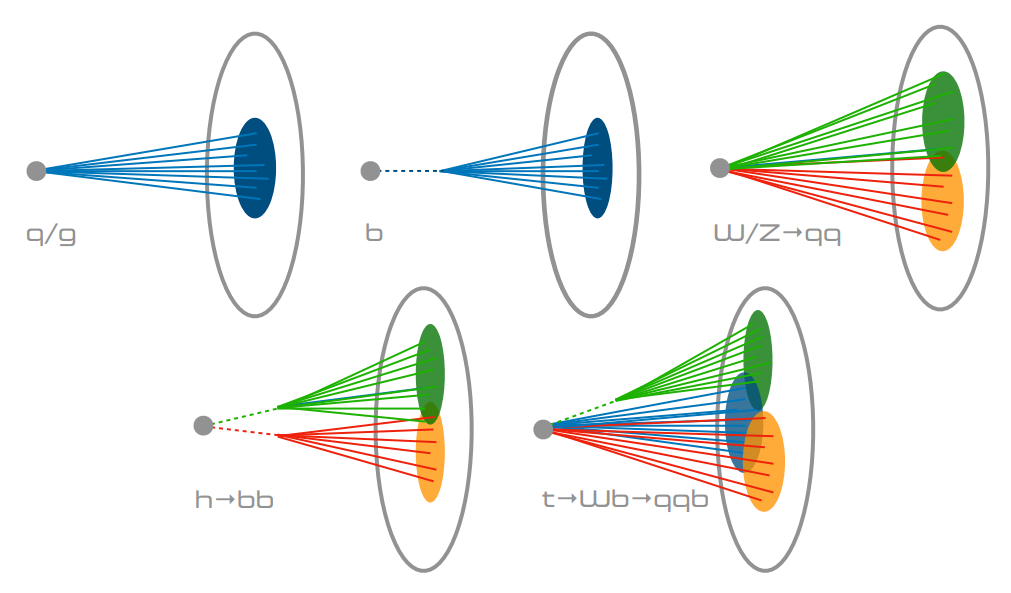
Figura 2.17 Representación de jets producto de: quarks y gluones (arriba a la izquierda), quark bottom (arriba en el centro), y topologías de jets impulsados: bosones de alto \(p_T\) W y Z (arriba a la derecha), bosón de Higgs (abajo a la izquierda) y quark top (abajo a la derecha) decayendo a un estado final de quarks[60].¶
Como se observa en la Figura 2.17, a alto momento transverso, un bosón, un quark top e inclusive una partícula de nueva física que decaiga a dos o más quarks, puede ser reconstruida como un jet único debido a que los productos de decaimiento se encuentran muy cercanos. A continuación se describirán algunas de las variables que se calculan para diferenciar entre jets provenientes de distintas partículas, utilizando como referencia [61].
2.5.2.1. Masa¶
La masa es la variable más evidente para discriminar entre jets provenientes de distintas partículas. La masa de un jet es cercana a la masa de la partícula de la cual se origina, asumiendo que los productos del decaimiento están contenidos en el jet. Está definida como la suma de la masa invariante de todos los constituyentes del jet, calculada a partir del cuadri-momento de cada constituyente.
La distribución de masa del jet se utiliza para diferenciar jets provenientes de partículas masivas con alto momento transverso, que se caracterizan por una distribución mas angosta y alta, de fondo que cae suavemente, debido a jets ordinarios de quarks y gluones[60]. En la Figura 2.18, se presenta un ejemplo de la distribución de la masa del jet principal de eventos provenientes de quarks y gluones, o fondo, y para una señal de nueva física con partículas de 500 y 100 GeV que decaen a jets.
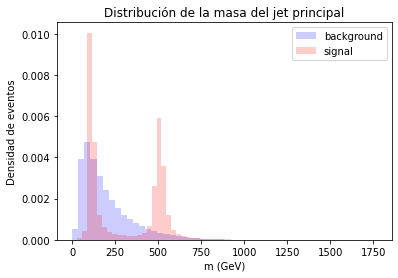
Figura 2.18 Distribuciones de la masa del jet principal para jets de quarks y gluones, o fondo, y de una señal de nueva física con partículas de 500 y 100 GeV.¶
2.5.2.2. N-subjettiness¶
Esta variable intenta diferenciar jets de acuerdo al número N de subjets que conforman un jet[62]. Para lograr esto, se hace un agrupamiento exclusivo de N jets, utilizando los constituyentes del jet, y se calcula la variable \(\tau_N\),
donde \(\Delta R_{min,i}\) es la menor distancia entre el constituyente i del subjet más cercano y \(d_0\) es la suma de \(p_T\) de todos los constituyentes multiplicada por el radio del jet, para obtener \(0<\tau_N<1\). Un valor menor de \(\tau_N\) corresponde a una cantidad de subjets igual a N o menor, mientras que un valor mayor indica más de N subjets. Sin embargo, se prefiere utilizar variables adimensionales:
Un jet con N-1 subjets tendrá un valor de \(\tau_{N,N-1}\) mayor a un jet conformado por N o más subjets. En la Figura 2.19, se presenta un ejemplo de la distribución de \(\tau_{21}\) para jets provenientes de quarks y gluones, o fondo, y para una señal de nueva física que decae a jets con una subestructura de 2 o más subjets.
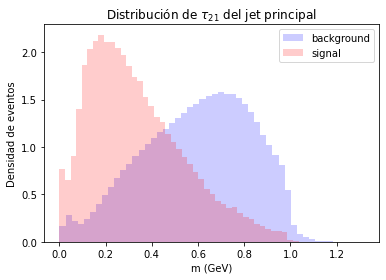
Figura 2.19 Distribuciones de \(\tau_{21}\) para jets de quarks y gluones, o fondo, y de una señal de nueva física con jets que tienen subestructura de 2 o más jets.¶
