4.3. Algoritmos LHCO 2020¶

Como se mencionó en la Sección 3.2, en las LHCO 2020 participaron 18 algoritmos agrupados dependiendo del tipo de método utilizados. En la Tabla 4.1 se encuentra un resumen de los participantes, con el método, referencias y los datos que analizaron.

Tabla 4.1 Grupos participantes de las LHCO 2020¶
Nombre	Método	Referencia	Resultado
VRNN	No supervisado	Artículo, Presentación	BB1-3
ANODE	No supervisado	Artículo, Presentación	R&D
BuHuLaSpa	No supervisado	Artículo	BB1-3
GAN-AE	No supervisado	GitHub, BumpHunter, Presentación	BB1-3
GIS	No supervisado	Artículo	BB1
LDA	No supervisado	GitHub, Artículo, Presentación	BB1-3
PGAE	No supervisado	GitHub	BB1,2
Reg. Likelihoods	No supervisado	Github modelo	R&D
UCluster	No supervisado	Github, Artículo	BB2,3
CWoLa	Débilmente supervisado	GitHub	BB1,2
CWoLa AE Compare	Débilmente/No supervisado	Artículo	R&D
Tag N” Train	Débilmente supervisado	GitHub, Artículo, Presentación	BB1-3
SALAD	Débilmente supervisado	GitHub, Artículo	R&D
SA-CWoLa	Débilmente supervisado	GitHub, Artículo	R&D
Deep Ensemble	Semi-supervisado	GitHub	BB1
Factorized Topics	Semi-supervisado	GitHub	R&D
QUAK	Semi-supervisado	Artículo	BB1-3
LSTM	Semi-supervisado	-	BB1-3

El rendimiento de los algoritmos participantes se puede comparar únicamente a través de los resultados obtenidos. Sin embargo, los grupos participantes analizaron diferentes conjuntos de datos, no todos reportaron un valor p, las masas de las partículas y el número de eventos de señal, criterios definidos en la Sección 3.2, y algunos resultados fueron reportados sin error. Además, los reportes referentes al rendimiento del modelo se hicieron en distintos formatos, de acuerdo al método utilizado. Por lo tanto, la comparación directa de los algoritmos es complicada.

Uno de los objetivos principales de este trabajo es comparar directamente algunos modelos participantes de las LHCO 2020. Para ello, es necesario poder reproducir el resultado de dichos modelos. Estos deben cumplir múltiples de los requisitos para hacer investigación reproducible, explicados en la Sección 3.3.2, para asegurar que se pueda obtener el resultado de los modelos en un tiempo adecuado para el desarrollo de este trabajo.

A continuación, se hablará del análisis de los algoritmos participantes a nivel de la reproducibilidad de sus resultados y se explicarán los modelos a comparar en este trabajo.

4.3.1. Reproducibilidad¶

Para escoger los algoritmos a comparar, se hizo una revisión extensiva de la información proporcionada por los grupos participantes mencionados en la Tabla 4.1. Como se explica en la Sección 3.3.2, para poder reproducir resultados en este contexto es necesario, principalmente, que se encuentre pública la información sobre el preprocesamiento de los datos, el código del modelo, instrucciones para utilizarlo, información del entorno computacional y licencia. Un resumen de la información proporcionada por cada grupo participante se encuentra en la Tabla 4.2,

Tabla 4.2 Información disponible de cada grupo participante de las LHCO 2020¶
Nombre	Preprocesamiento	Código	Instrucciones	Entorno	Licencia
VRNN	\(\checkmark\)	\(\checkmark\)	\(\checkmark\)	-	-
ANODE	-	-	-	-	-
BuHuLaSpa	-	\(\checkmark\)	-	-	-
GAN-AE	\(\checkmark\)	\(\checkmark\)	\(\checkmark\)	\(\checkmark\)	-
GIS	-	-	-	-	-
LDA	\(\checkmark\)	\(\checkmark\)	\(\checkmark\)	\(\checkmark\)	-
PGAE	\(\checkmark\)	\(\checkmark\)	\(\checkmark\)	\(\checkmark\)	-
Reg. Likelihoods	-	-	-	-	-
UCluster	\(\checkmark\)	\(\checkmark\)	\(\checkmark\)	\(\checkmark\)	\(\checkmark\)
CWoLa	-	\(\checkmark\)	-	-	-
CWoLa AE Compare	-	-		-	-
Tag N” Train	\(\checkmark\)	\(\checkmark\)	-	\(\checkmark\)	-
SALAD	-	\(\checkmark\)	-	\(\checkmark\)	-
SA-CWoLa	-	\(\checkmark\)	-	\(\checkmark\)	-
Deep Ensemble	-	\(\checkmark\)	\(\checkmark\)	\(\checkmark\)	-
Factorized Topics	-	\(\checkmark\)	-	-	\(\checkmark\)
QUAK	-	-	-	-	-
LSTM	-	-	-	-	-

Un resumen de general de la información proporcionada de todos los algoritmos se encuentra en la Figura 4.8

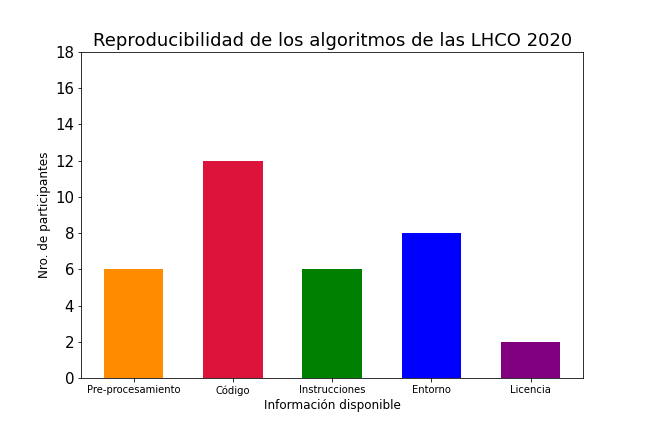
Figura 4.8 Resumen de la reproducibilidad de los participantes de las LHCO 2020.¶

En la Figura 4.8 se observa que pocos algoritmos participantes poseen información pública para poder reproducir sus resultados, lo que inmediatamente limita las opciones de modelos a utilizar en este trabajo. De acuerdo a la Tabla 4.2, de los 18 participantes, sólo UCluster cumple con todas las características. GAN-AE, LDA y PGAE cumplen con cuatro de las cinco características. Para este trabajo se escogieron UCluster y GAN-AE debido a la simplicidad de la información proporcionada. Los algoritmos se explicarán siguiendo [75].

4.3.2. UCluster¶

UCluster (Unsupervised Clustering)[107] es un método que reduce la dimensionalidad de los datos utilizando una red neuronal. El objetivo es retener las propiedades principales del evento de colisión, agrupando puntos con características similares que se encuentran inmersos en este espacio. El método es independiente de la arquitectura de la red neuronal.

Para crear la representación reducida de los datos (o encaje), se hace una clasificación de masa de jet por partícula, es decir, a cada partícula perteneciente a un jet se le asigna una etiqueta proporcional a la masa del jet al que pertenece. Estas etiquetas se crean definiendo 20 intervalos equidistantes entre 10 y 1000 GeV.

En particular, el modelo debe aprender la masa del jet al que la partícula pertenece y cuáles partículas pertenecen al mismo jet. El algoritmo utiliza las primeras 100 partículas asociadas a los dos jets más masivos de cada evento y consta de dos tareas: una de clasificación y otra de agrupamiento. La función de pérdida conjunta es:

(4.11)¶\[ L = L_{focal} + \beta L_{cluster}. \]

Un valor de \(\beta=10\) se utiliza para darle a las componentes el mismo orden de magnitud relativo. \(L_{focal}\) hace referencia a la función de pérdida focal, que es comúnmente utilizada para clasificar datos con etiquetas altamente desbalanceadas[75].

(4.12)¶\[ L_{focal}=-\frac{1}{N}\sum_j^N\sum_m^M y_{j,m}(1-p_{\theta,m}(x_j))^\gamma \log(p_{\theta,m}(x_j)), \]

donde \(p_{\theta,m}(x_j)\) es la confianza de la red para el evento \(x_j\), con parámetros entrenables \(\theta\), de ser clasificado como clase \(m\). \(y_{j,m}\) es 1 si la clase \(m\) es correctamente asignada al evento \(x_j\) y 0 de otra forma. Para las LHCO 2020, los participantes fijaron el parámetro \(\gamma=2\).

La función de pérdida del agrupamiento fue definida como,

(4.13)¶\[ L_{cluster}=\frac{1}{N}\sum_k^K\sum_j^N\|f_\theta(x_j)-\mu_k\|^2\pi_{jk}. \]

La distancia entre el evento \(x_j\) y el centroide \(\mu_k\) se calcula en el espacio de encaje \(f_\theta\), creado por la clasificación. \(\pi_{jk}\) pesa la importancia de cada evento para el objetivo de agrupación y está definido como:

(4.14)¶\[ \pi_{jk}=\frac{e^{-\alpha\|f_\theta(x_j)-\mu_k\|}}{\sum_{k'}e^{-\alpha\|f_\theta(x_j)-\mu_k\|}}, \]

con el hiperparámetro \(\alpha\).

El valor inicial de los centroides se obtiene utilizando el algoritmo K-means, para luego realizar el entrenamiento utilizando la función de pérdida conjunta en la ecuación (4.11).

Como se mencionó anteriormente, el modelo es libre de la arquitectura de la red neuronal. Sin embargo, la implementación utilizada en las LHCO 2020 utiliza ABCNet[108], una red basada en grafos donde cada partícula reconstruida es un nodo del grafo.

4.3.3. GAN-AE¶

El método GAN-AE intenta asociar un discriminante y un codificador automático como una red generativa antagónica siguiendo los pasos a continuación:

La red discriminativa es un perceptrón multicapas (MLP). Inicialmente es entrenado utilizando la entropía cruzada binaria (ec.(4.8)) en una muestra mezclada de eventos reconstruidos y originales, con el objetivo de exponer las debilidades del codificador automático.

El codificador automático es entrenado utilizando una función de pérdida que combina la reconstrucción del error, en este caso, la distancia euclídea media (MED, por sus siglas en inglés) entre la entrada y la salida y la entropía binaria cruzada.

(4.15)¶\[ \mathcal{L}_{AE} = \mathcal{L}_{BC}+\epsilon\times\text{MED}+\alpha\times\text{DisCo}, \]

donde \(\epsilon\) y \(\alpha\) son hiperparámetros para balancear los pesos de cada término y \(\text{DisCo}\) es la correlación de distancia, para decorrelacionar el error de reconstrucción de la masa invariante. En este caso, \(\mathcal{L}_{BC}\) se evalúa dando eventos reconstruidos a la red discriminativa, pero esta vez con la etiqueta «equivocada», con el objetivo de engañarla.

Por último, se evalúa el codificador automático utilizando una figura de mérito:

(4.16)¶\[ \text{FoM}=\text{MED}+(1-\text{Media salida MLP}). \]

El término \(1-\text{Media salida MLP}\) es cercano a cero a medida que el codificador automático engaña mejor al MLP.

Estos tres pasos se repiten en un bucle y una vez que el codificador automático ha sido entrenado se descarta la red discriminativa. Una vez descartada, el codificador automático utiliza las MED como característica discriminativa.

Los participantes utilizaron el método descrito anteriormente en conjunto con BumpHunter[109], un algoritmo que compara la distribución de los datos con datos de referencia y evalúa el valor p y la significancia de cualquier desviación. Sin embargo, la implementación en este trabajo se limita al uso del algoritmo GAN-AE, que es la parte de clasificación binaria de este método.

Búsqueda de nueva física utilizando técnicas de aprendizaje automático en eventos de múltiples jets

Algoritmos LHCO 2020

Contenido

4.3. Algoritmos LHCO 2020¶

4.3.1. Reproducibilidad¶

4.3.2. UCluster¶

4.3.3. GAN-AE¶